مفهوم مشتق و کاربردهای آن
مشتق مفهومی بسیار مهم در ریاضیات است که در علوم مختلف و خود ریاضیات کاربردهای فراوانی دارد و بسیار بسیار پر اهمیت است . مفهوم مشتق را در اصل میتوان یک مفهوم هندسی بیان کرد که آنرا به زبان فرمولاسیون ریاضی نیز بیان خواهیم کرد . در ادامه با مفهوم و کاربردهای آن بیشتر و کامل تر آشنا خواهیم شد.
ویدئو این مقاله
مفهوم مشتق
اگر بخواهم مفهوم مشتق را کامل بگویم ابتدا نیاز هست که یکم درباره شیب خط حرف بزنم . چونکه برای درک مفهوم مشتق باید از آن استفاده کرد . حالا خواهیم دید که اصلا مشتق یعنی شیب خط مماس در یک نقطه .
شیب خط
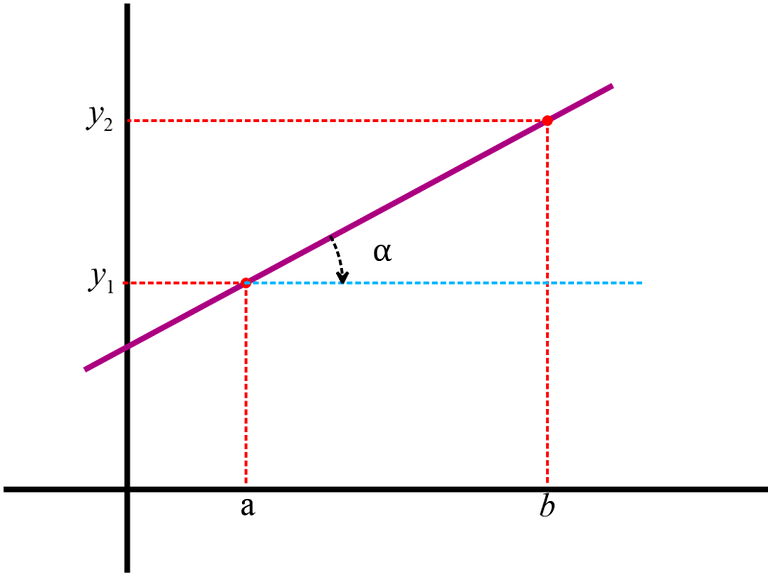
در دروس متوسطه اول و دوم با مفهوم شیب یک خط آشنا شده اید . وقتی نمودار یک تابع درجه اول را رسم میکردیم به یاد دارید که یک خط راست بود و با در دست داشتن مختصات دو نقطه از آن میتوانستیم شیب آنرا پیدا کنیم و حتی معادله خط را بنویسم .
این نمودار یک تابع درجه اول است که قبلا با آن آشنا شده اید . ما دو نقطه را داریم پس میتوانیم شیب آنرا بدست آوریم طبق فرمولی که در بالا نوشتم.
همچنین بخواهم بیشتر توضیح بدم شیب زاویه ای است که خط راست نمودار با محور طول ها ساخته است و ما برای برای طولی آن میتوانیم از تانژانت استفاده بکنیم که اگر تانژانت زاویه مشخص شده در شکل را بنویسیم:
$$\tan (\alpha ) = \frac{{\Delta y}}{{\Delta x}}$$
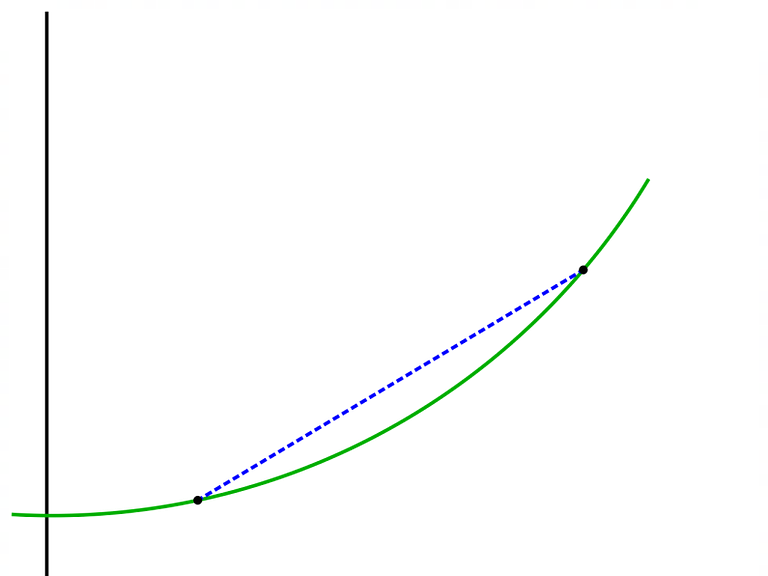
حالا که با مفهوم شیب خط آشنا شدیم برویم سراغ توضیح مفهوم مشتق . فرض کنید یک تابعی داریم که شکل نمودار آن بصورت زیر میباشد:
دو نقطه روی این منحنی را انتخاب کرده و خط واصل بین آنها را میکشیم . هر یک از این نقاط روی دستگاه مختصات ما جایگاهی دارند که میتوانیم مختصات آنها را بیان بکنیم یعنی طول و عرض نقاط را .
حال اگر بخواهیم شیب این خط واصل را با استفاده از آن نقاط ابتدایی و انتهایی بدست آوریم میتوانیم از فرمولی که در بالا نوشتم استفاده بکنیم .
حال فرض کنید من این نقاط روی نمودار را هی به هم نزدیک بکنم ، چه اتفاقی می افتد؟؟؟؟
اگر اینها هی به هم نزدیک شوند آن خط واصل ما هم تغییراتی دارد و از خط واصل به آن دو نقطه تبدیل میشود به خط مماس که میتوانید در شکل زیر ببنید
این از مفهوم هندسی مشتق و شیب خط . حال بیایید به بیان ریاضی فرمولی بگوییم اصطلاحا به بیان حسابانی بگوییم که مشتق یعنی چه . ما فرمول شیب خط را در بالا نوشتیم . اینجا هم گفتیم که این نقاط را به هم خیلی نزدیک میکنیم که این مفهوم حد است . حالا این چه معنی میده ؟ یعنی اینکه از فرمول شیب حد گرفتیم زمانی که نقاط به هم خیلی نزدیک شوند:
$$\mathop {\lim }\limits_{{x_2} \to {x_1}} \frac{{{y_2} – {y_1}}}{{{x_2} – {x_1}}} = f'(x)$$
این میشود فرمول مشتق که ما از آن استفاده خواهیم کرد برای پیدا کردن مشتق توابع و همچنین اثبات مشتق خیلی از توابعی که با آنها سروکار داریم از جمله مثلثاتی و درجه اول و درجه دوم و درجه سوم و…. .
کاربرد های مشتق
مشتق کاربرد های بسیار فراوانی دارد . مثالا در فیزیک ما برای بیان سرعت یک متحرک در لحظه از مفهوم مشتق استفاده میکنیم یا برای بیان شتاب یک جسم از مشتق استفاده میکنیم .
در شیمی مثلا برای بیان سرعت یک واکنش در لحظه میتوان از مفهوم مشتق استفاده کرد . حتی در علوم مهندسی مشتق مرتبه اول و دوم و سوم …. خیلی اهمیت دارد که باید با دقت تمام بررسی شوند . مشتق تنها این نیست و بسیاری از مفاهیم دیگر ریاضیات نیز به این مفهوم گره خورده از جمله مباحث بسیار مهم انتگرال و دیفرانسیل.
فرمول های مشتق
اگر بخواهیم فرمول و شکل اصلی فرمول مشتق را بنویسیم به دو صورت زیر میتوان نوشت که هر یک در جای خود کاربرد دارد اما هر دو یک مفهوم را میرسانند :
$$f'(x) = \mathop {\lim }\limits_{x \to a} \frac{{f(x) – f(a)}}{{x – a}}$$
$$f'(x) = \mathop {\lim }\limits_{h \to 0} \frac{{f(x + h) – f(x)}}{h}$$
مثال :
میخواهیم مشتق تابع زیر را پیدا بکنیم در نقطه ای به طول 2 .
$$f(x) = {x^2}$$
برای پیدا کردن متق این تابع از فرمول اول بهتر است اسفاده کنیم اما از دومی هم میتوان استفاده کرد . از اولی معمولا مواقعی استفاده میکنیم که بخواهیم مشتق در یک نقطه را پیدا بکنیم.
$$f'(2) = \mathop {\lim }\limits_{x \to 2} \frac{{f(x) – f(2)}}{{x – 2}}$$
$$f'(x) = \mathop {\lim }\limits_{x \to a} \frac{{f(x) – f(a)}}{{x – a}}$$
اگر 2 را به جای x قرار داهیم برابر حالت مبهم صفر صفرم خواهد شد که به راحتی میتوان رفع ابهام کرد .
$$f'(2) = \mathop {\lim }\limits_{x \to 2} \frac{{{x^2} – 4}}{{x – 2}} = \frac{0}{0} \to $$
$$\mathop {\lim }\limits_{x \to 2} \frac{{(x – 2)(x + 2)}}{{x – 2}} = \mathop {\lim }\limits_{x \to 2} (x + 2) = 2 + 2 = 4$$
مشتق توابع مهم
$$y=c\to \text{ }{y}’=0$$
$$[y=\text{ }{{x}^{n}}\text{ }\left( n\in \mathbb{Z} \right)\to \text{ }y\text{ }’\text{ }=n\text{ }{{x}^{n-1}}]$$
$$[y=\sqrt{x}\to {{y}’}=\frac{1}{2\sqrt{x}}]$$
$$[y=\sqrt[3]{x}\to \text{ }{y}’=\frac{1}{3\sqrt[3]{{{x}^{2}}}}]$$
$$[y=\sqrt[{}]{ax+b}\to \text{ }{y}’=\frac{a}{2\sqrt[{}]{ax+b}}]$$
$$[y=f(x)+g(x)\to \text{ }{y}’={f}'(x)+{g}'(x)]$$
$$[y=f(x)-g(x)\to \text{ }{y}’={f}'(x)-{g}'(x)]$$
$$[y=f(x).g(x)\to \text{ }{y}’={f}'(x).g(x)+f(x).{g}'(x)]$$
$$[y=\frac{f(x)}{g(x)}\to \text{ }{y}’=\frac{{f}'(x)g(x)-{g}'(x)f(x)}{{{g}^{2}}(x)}]$$
$$[\frac12\sqrt{5x-10}\sqrt[3]2]$$



11 نظر
سلام
خلی مفید بود . تشکر می شود
بسیار زیبا و روان و تو مخ برو توضیح دادید .
لطف دارید . خوشحالم مفید بوده
بسیار بسیار عالی توضیح دادید خیلی عالی
❤️سپاس از لطف شما
ممنون از شما، مفید، کوتاه، موجز👍
❤️سلامت باشید . خوشحالم که مفید بوده
شما تعریف دوم مشتق رو اشتباه نوشتید،برای آموزش باید بیشتر دقت کنید
ممنون از شما . اشتباه تایپی بود اصلاح شد .
بسیار بسیار عالی توضیح دادید خیلی عالی
سلامت باشید . خوشحالم که مفید بوده براتون