شیب خط و معادله خط
شیب خط و معادله خط در صفحه
شیب خط
تعریف شیب خط :نسبت ارتفاع به مسافت طی شده افقی را شیب خط گوییم
در این پست میخواهیم صفر تا100 شیب خط و معادله خط را بررسی بکنیم . برای پیدا کردن معادله یک خط در صفحه ما باید شیب آن خط را بیابیم . همانطور که در تعریف گفتیم :

$${m = a = \frac{h}{l}} $$
l : مسافت افقی طی شده
h : ارتفاع
اثبات شیب خط
میخواهم با استفاده از نمودار یک خط راست و توصیف هندسی آن به فرمول شیب خط برسیم که در ادامه نیز استفاده خواهیم کرد . یک نمودار خط راست را میبینید که با افق زاویه ای را ساخته است و میدانیم که :
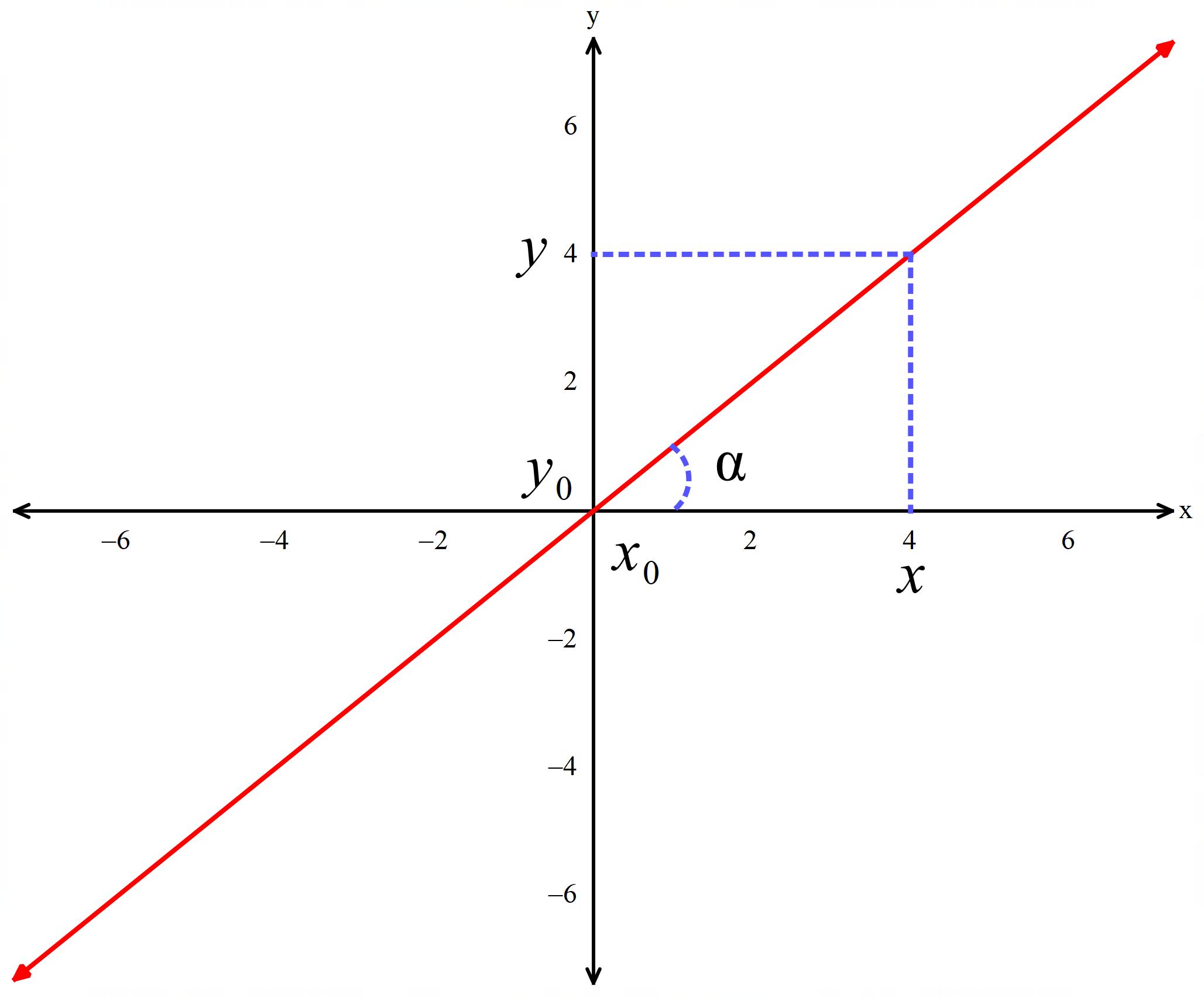
$$ l = x – {x_0}$$
$$ h = y – {y_0}$$
$$ m = \frac{h}{l} = \frac{{y – {y_0}}}{{x – {x_0}}} $$
$$ \tan (\alpha ) = \frac{h}{l} = \frac{{y – {y_0}}}{{x – {x_0}}} = m$$
این فرمول به ما شیب خط را میدهد که اگر مختصات دو نقطه از خطی را داشته باشیم میتوانیم با استفاده از این فرمول شیب این خط را در صفحه بدست آوریم .
با استفاده از فرمول زیر هم میتوانیم به صورت معکوس عمل کرده و زاویه خط با افق را پیدا بکنیم که از معکوس تانژانت استفاده خواهیم کرد .
$$\alpha = {\tan ^{ – 1}}(\frac{{y – {y_0}}}{{x – {x_0}}})$$
معادله خط
شیب خط را اثبات کردم و حالا نوبت میرسد به معادله خط نوشتن . برای نوشتن معادله خط از همان داده های بالا استفاده میکنیم .
$$ m = \frac{h}{l} = \frac{{y – {y_0}}}{{x – {x_0}}} $$
$$ \to y – {y_0} = m(x – {x_0})$$
$$ \to y = {y_0} + m(x – {x_0})$$
و این فرمول معرف معادله خط میباشد که خیلی راحت با استفاده از همان فرمول شیب خط و جابجایی ارکان آن توانستیم معادله خط در صفحه را بنویسیم . پس برای نوشتن این باید شیب خط و مختصات دو نقطه از خط را داشته باشیم . در ادامه چند تا مثال باهم ببنیم و نمودار های آنها را بررسی کنیم .
مثال )
میخواهیم شیب خط را برای این موارد تعیین بکنیم .
a) 3x +1
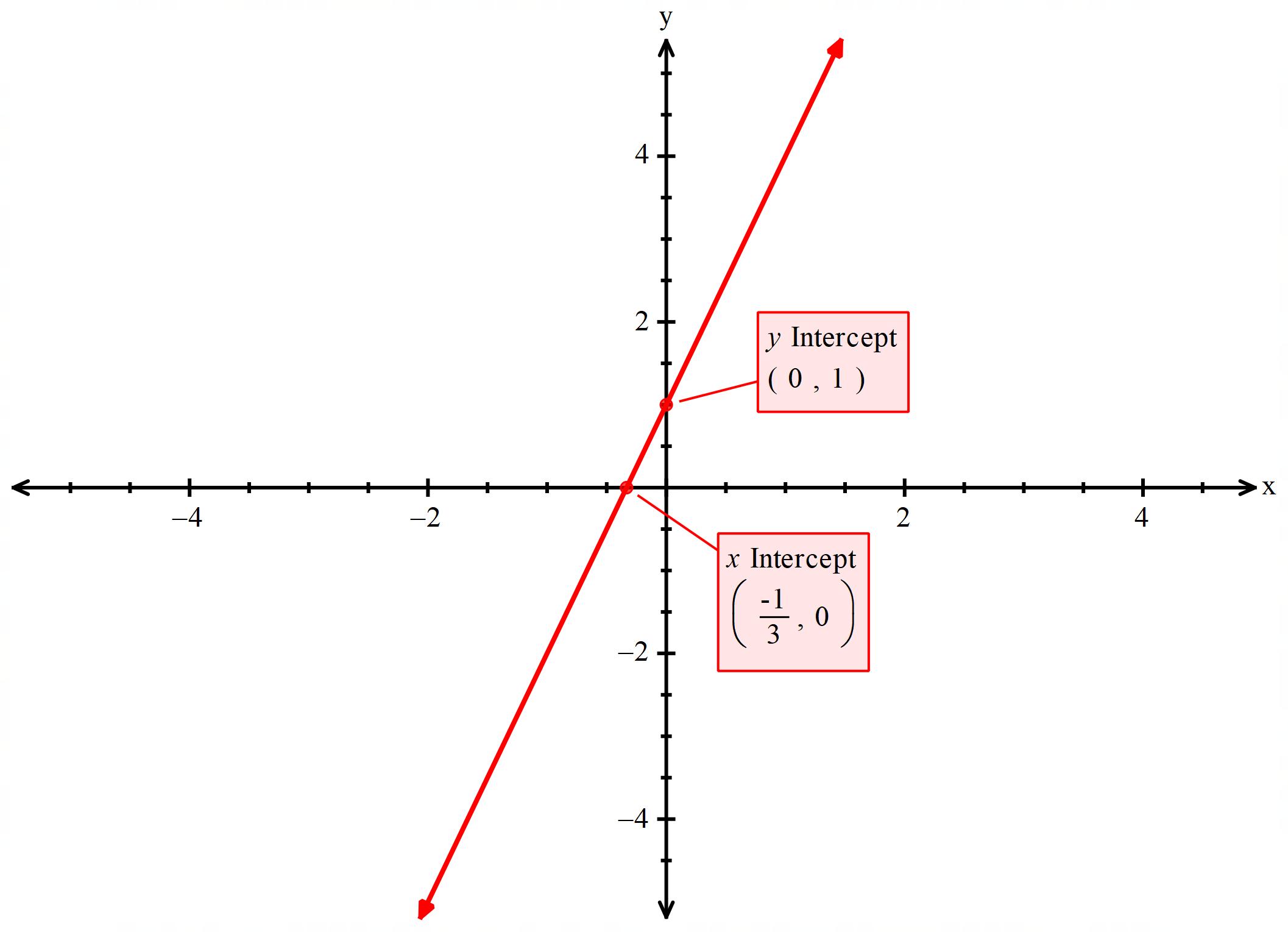
دو نقطه روی نمودار را تعیین میکنیم و با استفاده از آنها شیب را تعیین میکنیم.
نقاط مورد نظر را $$ ( – \frac{1}{3},0),(0,1) $$ میگیرم
$$ m = \frac{{y – {y_0}}}{{x – {x_0}}} \to m = \frac{{1 – 0}}{{0 – ( – \frac{1}{3})}}$$
$$ \to m = \frac{1}{{\frac{1}{3}}} = 3$$
b) y= -2x+2
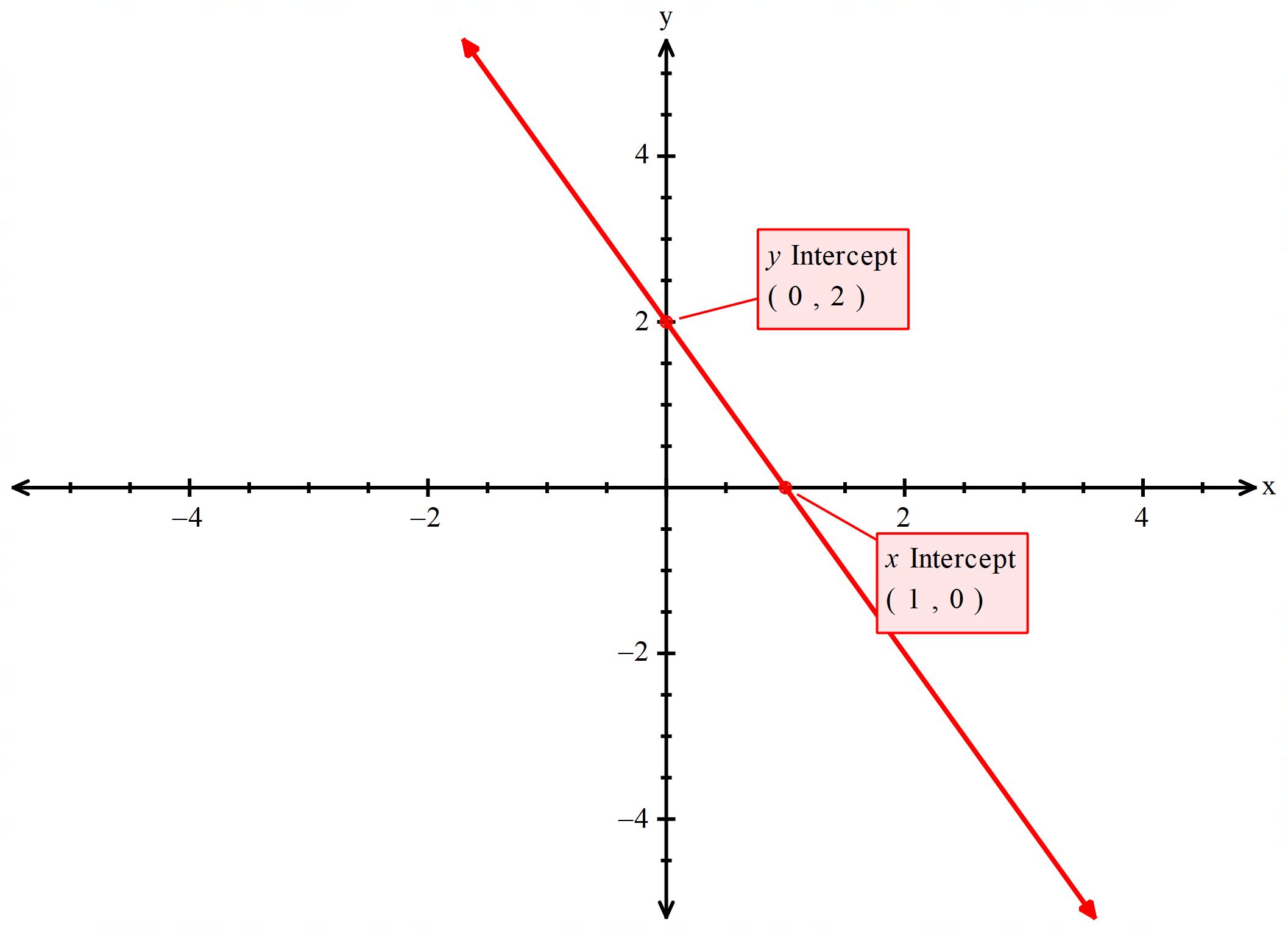
دوباره مثل مثال بالا دو نقطه از نمودار را انتخاب میکنیم و در فرمول شیب خط میگذاریم و شیب را بدست می آوریم .
$$m = \frac{{y – {y_0}}}{{x – {x_0}}} \to m = \frac{{2 – 0}}{{0 – 1}}$$
$$ \to m = \frac{2}{{ – 1}} = – 2$$

